voltar pagina inicial

Analise  de  Circuitos em Corrente Continua   
Aula07: Curva Característica de um Bipolo 

Bibliografia: 
Analise de Circuitos em Corrente Continua - Rômulo O. Albuquerque - Editora Érica
Analise e Simulação de Circuitos no Computador - MultSIM2001 - Rômulo O. Albuquerque - Editora Érica

Bipolo Linear  Bipolo Não Linear Experiência05  Exercício Resolvido 
Curva do Resistor Exercícios Propostos Curva do Diodo

1. Equação Característica - Curva Característica 

 Dado qualquer bipolo,  a relação matemática entre a tensão aplicada nele  e a corrente que o percorrerá é expressa através da sua equação característica, U =f(I) ou I =f(U),  isto é,  a tensão é dependente da corrente ( primeiro  caso )  ou a corrente  é dependente da tensão ( segundo caso ). Essa relação pode ser linear  ( bipolo linear )  ou não ( bipolo não linear ). 
Um exemplo de um bipolo linear é o resistor e  cuja equação característica é   U = R.I  e que poderia ser também  I = U/R,  em qualquer um dos casos a relação matemática  é uma relação de primeiro grau  do tipo y=a.x.

Um exemplo de um bipolo não linear é um diodo. Neste caso a relação entre corrente e tensão é  exponencial.

A representação gráfica da equação característica chamamos de curva característica. Por exemplo, seja um resistor de 100W. 
A equação característica desse resistor é : U =100.I     ou      I = U/100.
Para reapresentar graficamente essa equação, especificamos valores  para uma das variáveis ( por exemplo para I) e obtemos o valor da outra usando a equação.
Mas que valores usar ? Em principio, qualquer valor, mas  para tornar mais compatível com a realidade  é conveniente usarmos valores de acordo com os limites do componente. A seguir na figura1,  o circuito  para levantar a curva característica de dois resistores ( 100W e 200W)     e  a figura2 as curvas  correspondente.

Fig01: Circuito para obter a curva característica  do resistor                                   Inicio

É importante notar que a fonte deve ser ajustável permitindo mudar o valor da tensão.

  A seguir na figura2 temos os dois gráficos que representam as duas curvas.

Fig02: Curvas características dos resistores de 100W e 200W                                                       Inicio

Obs: Essas curvas foram obtidas usando o MicroCap

Tabela de valores

Tensão 100W 200W
U(V) I(mA) I(mA)
0 0 0
2 20 10
4 40 20
6 60 30
8 80 40
10 100 50

 

 Como podemos verificar, para cada valor de corrente temos um correspondente valor de tensão. A relação entre tensão e corrente é linear, isto é, se a  tensão dobrar de valor a corrente também dobrará.

A seguir na figura3 um exemplo de bipolo não linear e a sua curva.

          Fig03: Circuito para obter a curva característica  do diodo                                Inicio

Como a analise do componente chamado diodo não faz parte deste curso, nos restringiremos a fornece a curva e o símbolo.  

Fig04: Curva característica  do diodo- Bipolo Não linear                                                                                             Inicio

Obs: Essas curvas foram obtidas usando o MicroCap

2.Exercício Resolvido


1) É dado a curva característica de um  resistores. Pede-se determinar o valor da sua resistência.


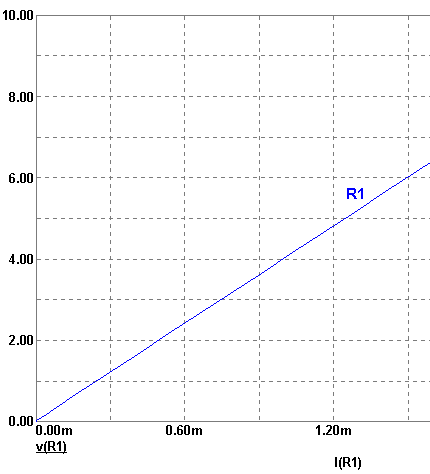R:  Como o bipolo é linear, basta um ponto do gráfico para determinarmos a sua resistência.

Para U=6V a corrente resultante é 1,5mA ( cada divisão vale 0,3mA ) , portanto o valor da resistência será  
R1 = 6V/2,5mA =4KW

2) Idem 1.                                                                                                                                            Inicio

R: Exatamente como no  exercício anterior ,  tendo um ponto teremos o valor  da resistência, no caso para U=20V  I = 2mA   portanto o valor da resistência será : R2 = 20V / 2mA  =10MW

3. Experiência05 - Curva Característica de um Bipolo

3.1.  Abra o arquivo ExpCC05 e identifique o circuito da figura5. Para cada valor de tensão da tabela meça a corrente no   resistor. Para obter uma tensão negativa coloque a chave R para cima ( pressione a letra R do teclado para mudar de posição ).

Fig05: Circuito para levantar a  curva UxI de um resistor                                          Inicio

Tabela I

U(V)    -4    

   -2    

    0         2          4     
I(mA)          

3.2. Com os dados da tabela I levante o gráfico de UxI ( U na vertical e I na horizontal ) em papel milimetrado .

3.3.  Abra o arquivo ExpCC05 e identifique o circuito da figura6. Para cada valor de tensão da tabela meça a corrente no   resistor. Para obter uma tensão negativa coloque a chave R para cima ( pressione a letra R do teclado para mudar de posição ).

               Fig06: Circuito para levantar a  curva IxU de um diodo

Tabela II

U(mV)   100     500     600     650     700     720     740     765     800     820  
I(mA)                    

3.4.  Com os dados da tabela II  levante o gráfico de IxU ( I na vertical e U  na horizontal ) em papel milimetrado .

4. Conclusões:

5. Exercícios Propostos

5.1) Dada a curva  de um resistor, podemos afirmar que a sua resistência vale:

a) 50W     a) 500W         a) 20W          a) 200W       a) 100W                                                      Inicio

5.2) Dada a curva  de um diodo, assinale  qual o valor da corrente para cada tensão dada na tabela.

     Tensão no diodo(V)  Corrente no diodo (A)
0.4 0.4 0.2 0
0.8 0.2 0.4 0.6
0.85 0.2 0.4 0.6

voltar pagina inicial

 

Fim da Página

 

 

 

 

 

 

 


IR PARA PÁGINA INICIAL

voltar para mais testes

 

A SUA RESPOSTA ESTÁ CORRETA !!!

 

 

 

 

 

 

 

 

 

 

IR PARA PÁGINA INICIAL

voltar para mais testes

A SUA RESPOSTA ESTÁ ERRADA !!!